Colaboradores - Cristiano Lehrer
Colaboradores
Cristiano Lehrer

1. Ybadoo
2. Colaboradores
3. Cristiano Lehrer
4. Artigos Científicos
5. O Uso da Metodologia de Superfície de Resposta para Adequar os Parâmetros de Entrada de um Algoritmo Genético

O Uso da Metodologia de Superfície de Resposta para Adequar os Parâmetros de Entrada de um Algoritmo Genético

Barbetta, Pedro Alberto; Lehrer, Cristiano. O Uso da Metodologia de Superfície de Resposta para Adequar os Parâmetros de Entrada de um Algoritmo Genético. Trabalho apresentado no XXI Encontro Nacional de Engenharia de Produção, Salvador/BA, 2001. 7 páginas.

Abstract

This paper describes the Response Surface Methodology (RSM), quite common in industrial processes optimization. It shows how the RSM being applied to optimize the choice of input parameters for a genetic algorithm. The application is very specific, but the same processes may be applied to more general computer systems.

01. Introdução

Desde os primórdios da investigação científica, realizavam-se experimentos para validar teorias e para levantar novas hipóteses sobre um mundo desconhecido. Mas foi a partir da década de 20, com os trabalhos de R. A. Fisher, que passou-se a ter uma metodologia confiável para planejar experimentos e analisar os seus dados. Grande parte dos trabalhos de Fisher eram voltados à agricultura, onde buscavam encontrar uma combinação adequada dos elementos de um fertilizante considerando o cultivo, o clima e o tipo de solo.

Na área industrial, especialmente nas duas últimas décadas, as técnicas de planejamento de experimentos passaram a fazer parte de programas de melhoria da qualidade. Esta prática deve-se muito aos trabalhos Box et al. (1978) e Taguchi (1987) que popularizaram os chamados projetos experimentais do tipo fatorial fracionado, os quais permitem avaliar grande número de fatores com poucos ensaios. Montgomery (1997) oferece uma apresentação bastante didática destes projetos.

A aplicação da metodologia de planejamento de experimentos na avaliação de sistemas computacionais é razoavelmente recente. Contudo, Jain (1991) já elegia o planejamento de experimentos como uma das principais ferramentas na avaliação de desempenho de sistemas computacionais. Muitos trabalhos, também, apoiam-se em sistemas computacionais para simular dados de algum processo, como descrito em Welch (1992), Mayer e Benjamin (1992) e Shang e Tadikamalla (1998), os quais projetam a simulação e realizam a análise dos dados sob a metodologia de planejamento de experimentos.

Barbetta (1998) e Barbetta et al. (2000) também apresentaram uma aplicação pouco comum de planejamento de experimentos ao aperfeiçoar um procedimento estatístico. A metodologia foi aplicada sob dois enfoques. Num primeiro momento, identificou-se os fatores mais relevantes do processo (fase de caracterização) e, depois, buscou-se a combinação de níveis dos fatores mais relevantes para maximizar o desempenho do processo (fase de otimização).

02. Otimização de Processos Através da Metodologia de Superfície de Resposta

A metodologia de superfície de resposta (RSM) pode ser entendida como uma combinação de técnicas de planejamento de experimentos, análise de regressão e métodos de otimização. Tem larga aplicação nas pesquisas industriais, particularmente em situações onde um grande número de variáveis de um sistema influencia alguma característica fundamental deste sistema.

Box et al. (1978) apresentam a RSM como uma metodologia que consiste num grupo de técnicas usadas em estudos empíricos. Estas técnicas relacionam uma ou mais respostas, tais como produção, tonalidade e viscosidade com variáveis de entrada, tais como tempo, temperatura, pressão e concentração. A RSM tem sido usada para responder questões do tipo:

1. Como uma resposta particular é afetada por um conjunto de variáveis de entrada sobre uma região de interesse?
2. Quais conjuntos de entradas geram um produto satisfazendo simultaneamente várias especificações desejadas?
3. Quais os valores de entradas que produzem o valor máximo para uma resposta específica e como se comporta a resposta em torno deste máximo?

Dado um processo ou sistema, com várias variáveis (ou fatores) de entrada, x = (x₁, x₂, ..., x_k)’ e uma variável de saída (ou resposta) y, a RSM normalmente consiste em:

1. planejar um experimento que permita estimar uma equação de regressão (superfície de resposta) do tipo E(y/x) = f(x, β), x ∈ D ⊂ ℜ^k, onde:
   • E(y/x) representa o valor esperado de y, condicionado a pontos x ∈ D;
   • f é uma função (usualmente um polinômio de grau não superior a 2);
   • x é o vetor de variáveis de entrada;
   • β é um vetor de parâmetros a ser estimado a partir dos dados do experimento;
   • D ⊂ ℜ^k é a região especificada para a investigação.
2. com os dados do experimento, estimar o vetor de parâmetros β, avaliando a significância estatística de seus componentes;
3. estudar o comportamento da função f (por exemplo, se é desejado o maior valor possível para a resposta y, um dos interesses é obter x₀ ∈ D que maximiza f, caso ele exista).

03. Modelo para a Variância

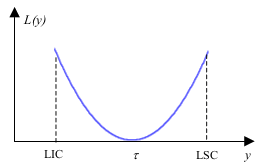
Considere um processo com valor ideal τ, mas, devido a efeitos aleatórios, o resultado obtido é um valor y. Por exemplo, uma empacotadora de café pode estar programada para encher pacotes com τ = 500 g, mas ao medir o peso de um pacote de café o valor observado deve ser y ≠ 500 g. A função perda quadrática é uma forma bastante usada para medir a perda da qualidade devida a variação em torno do valor ideal e é dada por

onde k é uma constante de proporcionalidade fazendo com que a função L assuma valores em termos monetários e [LIC, LSC] é o intervalo de especificação da característica y (ver Figura 1).

É natural o objetivo de minimizar o valor esperado da função perda, que é dado por

onde μ_y e σ_y² são o valor esperado e a variância de y, respectivamente.

Considerando que tanto a média quanto a variância sofrem influência de um vetor x’ = (x₁, x₂, ..., x_k) de fatores do processo, busca-se encontrar o vetor x₀ que minimiza a perda esperada ou, equivalentemente, que ajusta μ_y = f(x) ao alvo τ e minimiza σ_y² = g(x). Um passo importante deste processo de otimização é a construção de modelos para μ_y e σ_y² em função de x’ = (x₁, x₂, ..., x_k).

Para se construir um modelo para a média, μ_y = f(x), geralmente se aplica a análise de regressão tradicional, onde existe o método dos mínimos quadrados que é considerado pelos engenheiros quase como um padrão para efetuar a estimação dos parâmetros do modelo. O método pode ser aplicado diretamente sobre as observações de y ou sobre as médias, y_i (i = 1, 2, ..., n), calculadas em cada ponto experimental. Por outro lado, não se tem um procedimento de uso comum para estimar os parâmetros de um modelo para a variância, σ_y² = g(x).

Quando o número de replicações for grande (dez ou mais, segundo Bartlett e Kendall, 1946), um procedimento eficiente para construir o modelo para a variância do processo é calcular a variância amostral em cada ponto experimental ensaiado com replicações: S_i² (i = 1, 2, ..., n). Após uma transformação logarítmica, log(S_i²), usam-se estas estatísticas como se fossem observações numa análise de regressão tradicional. Outras abordagens são discutidas em Carroll e Ruppert (1988), Barbetta (1998) e Barbetta et al. (2000).

O modelo da variância pode ser usado isoladamente como uma forma objetiva para se conhecer os fatores que mais influenciam a variância e, com isto, buscar robustez em relação aos ruídos. Mas, também, o modelo da variância pode ser usado em conjunto com o modelo da média. Neste caso, busca-se uma solução de compromisso entre os objetivos de se levar a média ao alvo e de se minimizar a variância. Vining e Myers (1990) e Ribeiro e Elsayed (1995), por exemplo, apresentam técnicas interessantes para a obtenção de soluções de compromisso.

04. O Uso da Metodologia de Superfície de Resposta numa Aplicação de AG

Um problema típico em Engenharia de Produção é o chamado Problema do Caixeiro Viajante, que pode ser assim descrito: dadas n cidades, as distâncias entre elas e a cidade de origem e chegada, deve-se determinar a rota de menor distância total. Porém, quando n é grande, o número de possíveis rotas (soluções) torna-se extremamente grande e a avaliação de todas as rotas pode ser uma tarefa demorada até para os equipamentos computacionais atuais.

Para se obter uma boa solução e em pequeno tempo pode-se lançar mão de um algoritmo genético. Considera-se todas as possíveis combinações do conjunto {1, 2, ..., n} como a sequência de cidades a percorrer. É comum considerar o mesmo valor na primeira e última posição, que corresponde a cidade de origem e de destino final do caixeiro viajante. Na linguagem de algoritmos genéticos, uma combinação de {1, 2, ..., n} é chamada de cromossomo. E o algoritmo pode ser descrito assim:

1. Inicia-se com um conjunto (população) de k cromossomos viáveis (k permutações de {1, 2, ..., n});
2. Avalia-se o desempenho de cada cromossomo (total das distâncias entre cidades a percorrer);
3. Selecionam-se pares de cromossomos para participarem da nova geração, onde os cromossomos com melhor desempenho têm maior probabilidade de seleção;
4. Aplicam-se, com certa probabilidade, operações de crossover entre pares de cromossomos selecionados. Esta operação consiste em dividir um par de cromossomo em um ponto aleatoriamente escolhido e emendar cada um deles com a parte do outro, formando um novo par de cromossomos;
5. Aplicam-se, com certa probabilidade, a operação de mutação sobre algum gene do cromossomo gerado. Isto é, pode haver a alteração aleatória de um gene (cidade) do novo cromossomo;
6. Os novos cromossomos gerados constituem uma nova população e volta-se para o passo (b), a menos que um certo critério de parada seja satisfeito.

No presente trabalho, o número n de cidades foi fixado em 26, correspondendo às capitais brasileiras com exceção de Macapá. O número de iterações do algoritmo foi 10.000 e em cada iteração considerou-se 200 rotas possíveis. Já as probabilidades de crossover e mutação foram avaliadas por um projeto fatorial 3x3, ou seja, usou-se 3 diferentes probabilidades de crossover (fator A) e de mutação (fator B) cruzando-as, conforme ilustra a Figura 2.

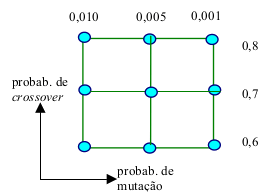
Em cada ponto experimental foram feitas 100 realizações do algoritmo e, para cada uma delas, anotou-se a solução (a menor rota a percorrer) e a correspondente distância total y. Considerou-se duas estatísticas baseadas nas 100 realizações de cada ponto experimental: a média aritmética (y_i, i = 1, 2, ..., 9) e o logaritmo natural da variância amostral (log(S_i²), i = 1, 2, ..., 9). O processo ainda foi repetido quatro vezes, tendo, na verdade, quatro valores de y e de log(S²) em cada ponto experimental, conforme mostra a Tabela 1.

Busca-se conhecer a combinação das duas probabilidades de entrada (mutação e crossover) que levam a valores pequenos de y e de log(S²). Para tanto, ajustou-se, por mínimos quadrados, funções quadráticas para as duas respostas consideradas, como segue:

onde X₁ e X₂ representam as probabilidades de crossover e de mutação, respectivamente. A qualidade do ajuste, medido pelo coeficiente de determinação R², foi de 0,63 para a equação (3) e 0,54 para a equação (4). A Figura 3 mostram as curvas de níveis das equações (3) e (4), que permitem encontrar as melhores probabilidades de crossover e de mutação para um problema do tipo em estudo.

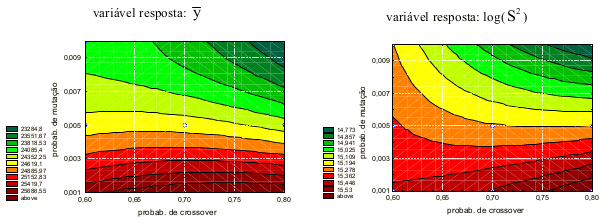
Como no presente caso é desejável que tanto y e quanto log(S²) sejam os menores possíveis, verifica-se que os melhores resultados são alcançados com probabilidade de crossover em torno de 0,8 e probabilidade de mutação em torno de 0,01.

05. Considerações Finais

O principal objetivo deste trabalho é mostrar como a metodologia planejamento de experimentos e de superfície de resposta podem ser usada para adequar parâmetros de entrada em sistemas computacionais. A aplicação do algoritmo genético no Problema do Caixeiro Viajante foi feita com vários dados de entrada fixados, mas pretende-se elaborar experimentos mais complexos, considerando, por exemplo, o número de cidades e as distâncias também como fatores variáveis no experimento. Com isso, pretende-se obter equações que, a partir dos dados de entrada de um particular problema, possa-se ter estimativas dos valores ideais dos parâmetros controláveis.

06. Referências Bibliográficas

Barbetta, P. A. (1998). Construção de Modelos para Médias e Variâncias na Otimização Experimental de Produtos e Processos. Tese (Engenharia de Produção), Florianópolis/SC.

Barbetta, P. A.; Ribeiro, J. L. D.; Samohyl, R. W. (2000). Variance Regression Models in Experiments with few Replications. Quality and Reliability Engineering International, Inglaterra, v. 16, p. 397-404.

Bartlett, M. S.; Kendall, D. J. (1946). The Statistical Analysis of Variance-Heterogeneity and the Logarithmic Transformation. Journal of the Royal Statistical Society, Series B, v. 8, p. 128-138.

Box, G. E. P.; Hunter, W. G.; Huter, J. S. (1978). Statistics for Experimenters. USA: John Wiley & Sons.

Carroll, R. J.; Ruppert, D. (1988). Transformation and Weighting in Regression. USA: Chapman and Hall.

Jain, R. (1991). The Art of Computer Systems Performance Analysis: techniques for experimental design, measurement, simulation, and modeling. USA: John Wiley & Sons.

Lehrer, C. (2000). Operador de Seleção para Algoritmos Genéticos Baseado no Jogo Hawk-Dove. Dissertação (Ciência da Computação), Florianópolis/SC.

Mayer, R. J.; Benjamin, P. C. (1992). Using the Taguchi Paradigm for Manufacturing System Design Using Simulation Experiments. Computers and Industrial Engineering, v. 22, n. 2, p. 195-209.

Montgomery, D. C. (1997). Design and Analysis of Experiments, 4 ed., USA: John Wiley & Sons.

Myers, R. H.; Carter, W. H. (1973). Response Surface Techniques for dual Response Systems. Technometrics, v. 15, n. 2, p. 301-317.

Myers, R. H.; Montgomery, D. C. (1995). Response Surface Methodology: process and product optimization using designed experiments. USA: John Wiley & Sons.

Ribeiro, J. L. D.; Elsayed, E. A. (1995). A Case Study on Process Optimization Using the Gradient Loss Function. International Journal of Production Research, v. 33, n. 12, p. 3233-3248.

Shang, J. S.; Tadikamalla, P. R. (1998). Multicriteria Desin and Control of a Celular Manufacturing System Through and Optimization. International Journal of Production Research, v. 36, n. 6, p. 1515-1528.

Taguchi, G. (1987). System of Experimental Design: engineering methods to optimize quality and minimize costs. 2 ed. USA: UNIPUB.

Vining, G. G.; Myers, R. H. (1990). Combining Taguchi and Response Surface Philosophies: a dual response approach. Journal of Quality Technology, v. 22, n. 1, p. 38-45.

Welch, W. J.; Buck R. J.; Sacks, J.; Wynn, H. P.; Mitchell, T. J.; Morris, M. D. (1992). Screening, Predicting and Computer Experiments. Technometrics, v. 34, n. 1, p. 15-25.

Download

Artigo científico apresentado no XXI Encontro Nacional de Engenharia de Produção